Capacitor Charging- Explained

The capacitor charging cycle that a capacitor goes through is the cycle, or period of time, it takes for a capacitor to charge up to a certain charge at a certain given voltage.

In this article, we will go over this capacitor charging cycle, including:

Capacitor Charging Capabilities
Capacitor Charge Equation
Capacitor Charging Graph

Before we go over the details, such as of the formula to calculate the voltage across a capacitor and the charging graph, we will first go over the basics of capacitor charging.Capacitor Charging Capabilities

How much a capacitor can charge to depends on a number of factors.

First, the amount of charge that a capacitor can charge up to at a certain given voltage depends on the capacitor itself. How much charge a capacitor can retain and at what voltage is determined by the specifications of the capacitor. Different capacitors have different charge capacities. Capacitors come in a whole range of capacitance capabilities. There are capacitors that can hold 1 picofarad of charge (10_-12 C) and there are other capacitors that can hold 4700µF of charge. So the amount that a capacitor can charge depends on the capacitor at hand. The same thing applies for the amount of voltage that it holds. Both capacitance and voltage depend on the internal construction of the capacitor. The capacitance and voltage capabilities of capacitors are specified for all capacitors. For electrolytic capacitors, these ratings are specified on the capacitor itself.

A capacitor will always charge up to its rated charge, if fed current for the needed time. However, a capacitor will only charge up to its rated voltage if fed that voltage directly. A rule of thumb is to charge a capacitor to a voltage below its voltage rating. If you feed voltage to a capacitor which is below the capacitor's voltage rating, it will charge up to that voltage, safely, without any problem. If you feed voltage greater than the capacitor's voltage rating, then this is a dangerous thing. The voltage fed to a capacitor should not exceed its rated value.

This is just a background on capacitor charge and voltage. Now we go on the equation to calculate capacitor voltage.

Capacitor Charge Equation

The Capacitor Charge Equation is the equation (or formula) which calculates the voltage which a capacitor charges to after a certain time period has elapsed.

Below is the Capacitor Charge Equation:

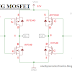
To charge a capacitor, a power source must be connected to the capacitor to supply it with the voltage it needs to charge up. A resistor is placed in series with the capacitor to limit the amount of current that goes to the capacitor. This is a safety measure so that dangerous levels of current don't go through to the capacitor.Below is a typical circuit for charging a capacitor.

Variables in Capacitor Charge Equation

Taken into account the above equation for capacitor charging and its accompanying circuit, the variables which make up the equation are explained below:

• VC- VC is the voltage that is across the capacitor after a certain time period has elapsed.
• VIN- VIN is the input voltage which is connected to the capacitor which supplies it with voltage, so that the capacitor can charge up. Without VIN, a power source, a capacitor cannot charge. Capacitors can only store voltage which they are supplied through a power source. The larger VIN , the greater the voltage the capacitor charges to, since it is being supplied greater voltage. Conversely, the smaller VIN, the smaller the voltage that the capacitor charges to, since it is being supplied with less voltage.
• Time, t- Time, t, is the period of time which has elapsed since the charging process begins. t is measured in unit seconds. It is a very important parameter in this equation because it determines how much the capacitor charges. The more time that has elapsed, the more the capacitor will charge. Conversely, the less time that has elapsed, the less the capacitor will charge.
• Resistance, R- R is the resistance of the resistor to which the capacitor is connected to in the circuit, as shown in the diagram above. This affects the charging process in that the greater the resistance value, the slower the charge, while the smaller the resistance value, the quicker the charge, and, thus, the lower the amount of voltage, VC, across the capacitor. This is because resistance represents an impedement. It slows down and lessens current, so that charging is slower, and, thus, the resultant voltage across the capacitor will be less than with a lesser resistance.
• Capacitance, C- C is the capacitance of the capacitor in use. C affects the charging process in that the greater the capacitance, the more charge a capacitor can hold, thus, the longer it takes to charge up, which leads to a lesser voltage, VC, as in the same time period for a lesser capacitance.

These are all the variables explained, which appear in the capacitor charge equation.

Again, if you want a quicker charge time for a RC circuit, use a small resistance value for the resistor, a small capacitance value for a capacitor, and a lower input voltage across the capacitor before discharge begins, for the variables you can control, for the reasons explained above.

If you want a longer discharge time for an RC circuit, use a large resistance value, a large capacitance value, and a large input voltage across the capacitor.

The charge time which you'll need depends on the specific application for which the RC circuit is used for.

Capacitor Charging Graph

The Capacitor Charging Graph is the a graph that shows how many time constants a voltage must be applied to a capacitor before the capacitor reaches a given percentage of the applied voltage.

A capacitor charging graph really shows to what voltage a capacitor will charge to after a given amount of time has elapsed.

Capacitors take a certain amount of time to charge. Charging a capacitor is not instantaneous. Therefore, calculations are taken in order to know when a capacitor will reach a certain voltage after a certain amount of time has elapsed.

The time it takes for a capacitor to charge to 63% of the voltage that is charging it is equal to one time constant. After 2 time constants, the capacitor charges to 86.3% of the supply voltage. After 3 time constants, the capacitor charges to 94.93% of the supply voltage. After 4 time constants, a capacitor charges to 98.12% of the supply voltage. After 5 time constants, the capacitor charges to 99.3% of the supply voltage.

The graph below shows all these transitions of capacitor charging time: